Simple Refutation of Special Relativity by Light Clock
Wolfgang G. Gasser
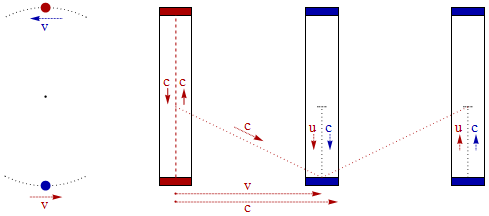
Fig. 1: On the left, two light-clocks circling horizontally a common center with each speed v = 0.9 c relative to the opposite clock. On the right, the vertical light-speed signals within both clocks with respect to the red clock assumed at rest. Light-speed c within and for the blue clock seems for the red clock only u = c /γ with Lorentz factor y= 0.44, due to time-slowing of the blue clock. Vector addition of vectored u und v then results in signal speed c =√ (v2 + u2). Thus for the red clock during 1 sec, only 0.44 sec of the blue clock elapse.
Two opposite light clocks with vertical light-path circle horizontally their common center, with a mutual relative speed of v = 0.99995 c. Lorentz factor γ = 1 / √(1 - v2/c2) results in 100. Applying the simple and transparent light-clock reasoning, we get:
With respect to each light-clock the light signal in the opposite clock (composed of vertical inside-clock movement u and horizontal movement v) can only propagate at c, if the rate of the opposite clock is γ = 100 times lower than the own clock rate.
If the height of such a light-clock with vertical light-path is e.g. 15 cm then one cycle lasts 2 ∙ 15 cm /c = 1 nanosecond. Our concrete thought experiment entails: Light-speed c can only be constant with respect to both clocks, if each to 100 own clock cycles corresponds only one cycle of the opposite clock, which is a logical impossibility.
In order to understand the principle of the contradiction, let us change the thought experiment and assume that the two light-clocks orbit on a regular hexagon. Let us further assume that traversing one segment lasts 1000 clock cycles (and the full orbit 6000 cycles).
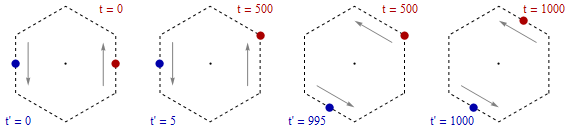
Fig. 2: Leap in time from t' = 5 to t' = 995 of the blue light-clock with respect to the red clock at t = 500.
Let us start with t = 0 and t' = 0 when both clocks are at the center of opposite hexagon segments. Due to symmetry, we have simultaneity of the two clocks. 500 own clock cycles later, each clock reaches the end of the segment. But to these 500 own clock cycles correspond only 5 cycles of the opposite clock (because of time slowing with γ = 100).
Just before entering the next hexagon segment at t = 500, the opposite clock shows t' = 5 and is thus 495 clock cycles in the past. Just after having changed direction (still at t = 500), the opposite clock shows t' = 995 and is 495 cycles in the future. When reaching the center of the new segment at t = 1000, simultaneity of the two clocks reigns again, since with t' = 1000 we have the same symmetrical situation as at the beginning.
This means that during every direction-change (such as at t = 500) the opposite clock accomplishes 990 clock cycles (such as from t' = 5 to t = 995). Thus, the attempt to guarantee constancy of c with respect to both light-clocks during inertial movement leads to an absurdly high or even infinite light speed within the opposite clock when changing direction.
(That the opposite clock remains at almost the same position from t = 0 to t = 500 is related to relativistic velocity addition. Both clocks move at u = 0.99 c relative to the hexagon center, as v = 2 u / (1 + u2) = 0.99995 c. Thus, for one clock the velocity of opposite clock is only by 0.00995 c higher than the velocity of the hexagon center.)
Summary:
In the case of hexagonal movement, constancy of light-speed is possible for both light-clocks during straight movement, because mutual time slowing is possible. Yet every change in direction leads to a time-leap-into-the-future of the opposite clock. The combination of continuous time slowing and discontinuous time-leaps leads on average to t' = t.
In the case of circular movement, time slowing of the opposite clock is continuously compensated by a continuous drift into the future due to continuous own direction-changes. This is in agreement with the requirement of symmetry between t and t', but it obviously violates constancy of light-speed for both light-clocks.
Special Relativity became thriving because it explains light-speed constancy on Earth, despite the Earth's orbit around the Sun at v = 0.0001 c. The SR explanation is essentially based on the light-clock reasoning. If the latter cannot explain light-speed constancy for both Earth and Sun, then SR is simply wrong, despite being based on effective and prolific scientific hypotheses.
People feigning or honestly trying to rescue Special Relativity from logical contradictions by claiming its inapplicability in case of accelerated movements are completely inconsequential and have no idea about the history of physics. The most important prediction resp. explanation of SR was just: Light-speed constancy in all directions despite the Earth's orbit around the Sun at v = 30 km/s = 4p3 m/s.
Inertial frames do not exist, nowhere in the Universe. Only accelerated movements do exist, such as e.g. the movement of a laboratory on Earth. Thus, if Special Relativity is only valid in the absence of accelerations, then the theory's range of validity is practically zero in the real world!
The movement of a laboratory near the equator consists of at least three accelerated movements:
- Diurnal rotation at 460 m/s = 2p46 m/s
- Rotation around the Sun at 30 km/s = 4p3 m/s
- Rotation around the galactic center at e.g. 220 km/s = 5p22 m/s
The SR conclusion "light-speed isotropy" on Earth is
applied in case of solar and galactic rotation, as the corresponding speeds do
not show up in experiments. (Cause: reference frames for light-speed are
dragged by the Earth's mass according to the 1/r2 law). In the case
of equatorial rotation however, it is assumed that the measured light-speed is
influenced by the Earth's diurnal rotation due to the Sagnac effect: Light speed in our laboratory is assumed to be c - 460 m/s ≈ 8p300 m/s - 2p46 m/s
from East to West, and c - 460 m/s ≈ 8p300
m/s + 2p46 m/s from West to East. The East-West asymmetry has
"officially" been confirmed in the Michelson-Gale
experiment of 1925.
An "unofficial" confirmation consists in the "persistent
spurious signal" found by Brillet and Hall, 1978.
Unfortunately these two crucial experiments have not been repeated. Instead,
the next generation of light-speed
isotropy experiments
has been designed in such a way that a light-speed
anisotropy due to the diurnal rotation cannot show up and spoil the desired
result of an "isotropy" (constancy in all directions) as high as
possible. Also possible isotropy-deviations due to our movement relative to the
sun are removed right at the outset of such experiments (mostly by averaging
techniques). And the huge light-speed anisotropy which must occur on the
International Space Station (light-speed ranging from around c – 7.5 km/s ≈ 8p300 m/s – 3p75 m/s to c + 7.5 km/s ≈
8p300 m/s + 3p75 m/s) has never been examined,
or is kept quiet, or assumed an unimportant Sagnac effect.
In order to make the problem presented above even more explicit and vivid, let
us imagine two spacecrafts each moving at v = 0.995 c = 9n995 c (with
Lorentz-factor γ = 10) towards Meeting point:
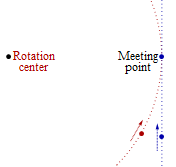
The red spacecraft moves on a circular orbit around Rotation center (in the absence of gravitation). The blue spacecraft moves on a straight line in such a way that the two spacecrafts will be side by side at Meeting point. According to the by far most widespread interpretation of SR (already advocated by Einstein 1905), a clock at Rotation center must run fast by factor 10 with respect to the circling spacecraft. Yet with respect to the blue spacecraft, the same clock at Rotation center goes slowly by factor 10. Yet on the other hand, since both spacecrafts are side by side and move in the same direction, clock rate at Rotation center must be the same with respect to both spacecrafts and cannot differ by factor 100 = γ2.
---
Fundamental scientific progress works by restructuring previous knowledge and not by incremental addition of new findings and theories
The following are contributions to discussions which can be found via groups.google.com – Same topic in German
The Simplest Refutation of Special Relativity – 2007-01-02
Two distant observers with each a (transversal) light clock orbit at a constant distance around their common center (assumed at rest).
Special relativity postulates that the light beams in both light clocks propagate at c relative to both (almost inertial moving) observers. This requires that for each observer the clock rate of the opposite clock must be lower than the clock rate of his own clock.
Because of symmetry and unchanging distance, clock rate cannot differ. The impossibility of mutual time dilation in this situation entails the impossibility of a constant speed of light as a general law.
2007-01-04
Tom Roberts:
For approximately inertial motion, the basic equations of SR are only APPROXIMATELY valid. You ignored the approximation you, yourself, made.
Let us assume a relative speed of v = 0.99995 c (with gamma = 100) of each observer with respect to the other. Deviation from inertial motion can be made as small as we like by choosing a large enough radius of the orbit in relation to the height of the light clock.
Applying the simple and transparent LIGHT CLOCK reasoning, we get:
With respect to each observer the light beam in the opposite clock can only propagate at c, if the rate of this clock is gamma = 100 times lower than the observer clock rate*. On the other hand, if the clock rates of both light clocks are equal, then with respect to each observer the velocity of the beam in the opposite clock is composed of the two orthogonal components c and v, resulting in a speed of light of cv = √[v2 + c2] = 1.41 c.
So we have a real contradiction and not something caused by an approximate calculation.
At a deeper level, however, such orbiting observers cannot be treated as inertial observers, because a circle is different topologically from a line.
Also this attempt to remove the contradiction leads to an untenable consequence: Let us assume that at a given moment the observers start moving inertial instead of further orbiting. When still orbiting, the time of each observer runs identically with respect to the other. Just after the start of inertial movement however, the time of each observer runs one hundred times slower with respect to the other!
* This gamma time dilation leads to a gamma reduction in the speed of the opposite clock beam from c to c/gammav. This opposite clock is moving at v with respect to the observer, and this movement is orthogonal to the light beam direction. Therefore the velocity of the beam with respect to the opposite observer results in the hypotenuse of the right-angled triangle with the legs v and c/gammav, and we get: cv = sqrt[v2 + (c/gammav)2] = sqrt[v2 + (c∙sqrt[1-v2/c2])2] = c
Daryl McCullough:
If the clocks are in circular orbits, then deviation from inertial motion is not negligible.
Do you understand the light clock reasoning? See for instance.
The light clock reasoning is EQUIVALENT to the SR constancy of the speed of light. So if in a certain situation the light clock reasoning cannot be applied without contradiction, then also c cannot be constant. The Lorentz transformation ensures the constancy of light not by some kind of magic, but by a very concrete and even transparent mechanism.
If the height of the light clock is 15 cm, then one cycle of the light clock lasts 2 * 15 cm / c = 1 nanosecond. In our concrete thought experiment that implies: c can only be constant with respect to both observers, if to one hundred clock cycles (100 ns) of the own clock corresponds only one cycle (1 ns) of the opposite clock.
So all the necessary happens within 100 ns, and therefore within a relative movement of less than 300 m. Compare these 300 m with e.g. the earth-sun distance (150 000 000 km).
Let us change the thought experiment and assume that the two observers orbit on a regular hexagon and are always exactly opposite with respect to the center of the hexagon. Let us further assume that traversing one segment lasts 1000 clock cycles (and the full orbit 6000 cycles).
Let us start with the situation when both observers (moving anti-parallel) are at the center of opposite hexagon segments. In this situation simultaneity is the same with respect to both observers and to the center of the hexagon. 500 own clock cycles later, each observer reaches the end of the segment. But to these 500 own clock cycles correspond only 5 cycles of the opposite clock (gamma = 100). So just before entering the next hexagon segment, the opposite clock is 495 clock cycles in the past. Just after having changed direction (in order to move along the next segment) however, the opposite clock is 495 cycles in the future.
This means that during change of direction the opposite clock accomplishes 990 actual clock cycles. So the attempt to guarantee constancy of c with respect to both observers during inertial movement leads to an absurdly high or even infinite light speed in the opposite light clock when changing direction.
Interestingly, my refutation of Special Relativity is somehow similar to a failed solution of the twin paradox by Einstein:
"Einstein addressed the twin paradox in special relativity in a relatively unknown, unusual and rarely cited paper written in 1918, in the form of a dialogue between a critic and a relativist. Contrary to most textbook versions of the resolution, Einstein admitted that the special relativistic time dilation was symmetric for the twins, and he had to invoke, asymmetrically, the general relativistic gravitational time dilation during the brief periods of acceleration to justify the asymmetrical aging." (Source)
What is not legitimate is to use the Lorentz transformations, because those are only valid for transformations between inertial coordinate systems.
Do you mean that Special Relativity does not explain the Michelson-Morley experiment? "Transformations between inertial coordinate systems" are certainly not applicable to the sun-earth system.